Time-Frequency-Polarization analysis: tutorial¶
This tutorial aims at demonstrating different tools available within the
timefrequency module of BiSPy. The examples provided here come
along with the paper
Julien Flamant, Nicolas Le Bihan, Pierre Chainais: “Time-frequency analysis of bivariate signals”, In press, Applied and Computational Harmonic Analysis, 2017; arXiv:1609.0246, doi:10.1016/j.acha.2017.05.007.
The paper contains theoretical results and several applications that can be reproduced with the following tutorial. A Jupyter notebook version can be downloaded here.
Load bispy and necessary modules¶
import numpy as np
import matplotlib.pyplot as plt
import quaternion # load the quaternion module
import bispy as bsp
Quaternion Short-Term Fourier Transform (Q-STFT) example¶
To illustrate the behaviour of the Q-STFT, we construct a simple signal made of two linear chirps, each having its own instantaneous polarization properties.
First, define some constants:
N = 1024 # length of the signal
# linear chirps constants
a = 250*np.pi
b = 50*np.pi
c = 150*np.pi
Then define the instantaneous amplitudes, orientation, ellipticity and phase of each linear chirp. The amplitudes are taken equal - just a Hanning window.
# time vector
t = np.linspace(0, 1, N)
# first chirp
theta1 = np.pi/4 # constant orientation
chi1 = np.pi/6-t # reversing ellipticity
phi1 = b*t+a*t**2 # linear chirp
# second chirp
theta2 = np.pi/4*10*t # rotating orientation
chi2 = 0 # constant null ellipticity
phi2 = c*t+a*t**2 # linear chirp
# common amplitude -- simply a window
env = bsp.utils.windows.hanning(N)
We can now construct the two components and sum it. To do so, we use the
function signals.bivariateAMFM to compute directly the quaternion
embeddings of each linear chirp.
# define chirps x1 and x2
x1 = bsp.signals.bivariateAMFM(env, theta1, chi1, phi1)
x2 = bsp.signals.bivariateAMFM(env, theta2, chi2, phi2)
# sum it
x = x1 + x2
Let us have a look at the signal x[t]
fig, ax = bsp.utils.visual.plot2D(t, x)
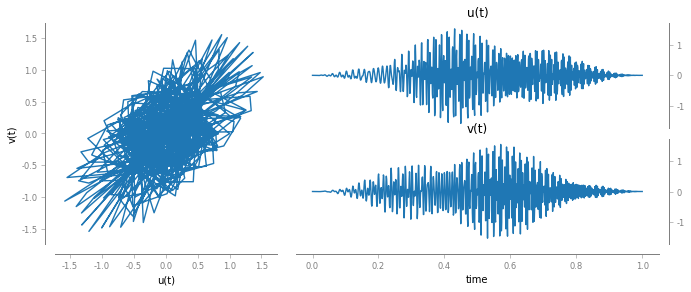
Now we can compute the Q-STFT. First initialize the object Q-STFT
S = bsp.timefrequency.QSTFT(x, t)
And compute:
S.compute(window='hamming', nperseg=101, noverlap=100, nfft=N)
Computing Time-Frequency Stokes parameters
Let us have a look at Time-Frequency Stokes parameters S1, S2 and S3
fig, ax = S.plotStokes()
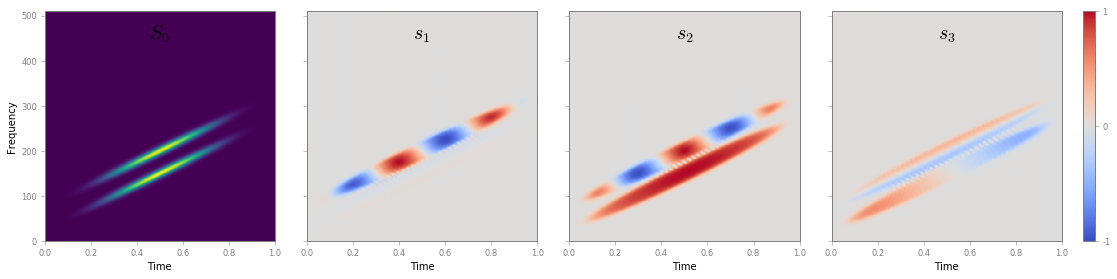
Alternatively, we can compute the instantaneous polarization properties from the ridges of the Q-STFT.
Extract the ridges:
S.extractRidges()
Extracting ridges
Ridge added
Ridge added
2 ridges were recovered.
And plot (quivertdecim controls the time-decimation of the quiver
plot, for a cleaner view):
fig, ax = S.plotRidges(quivertdecim=30)
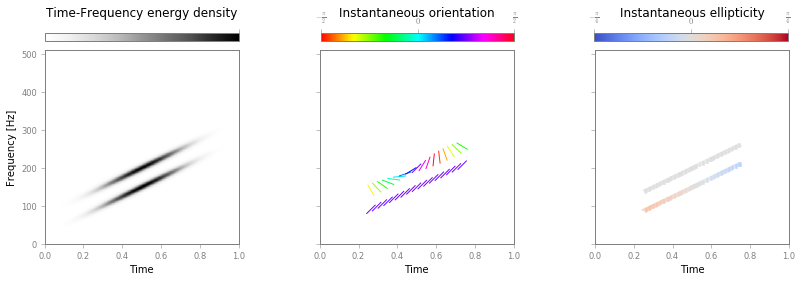
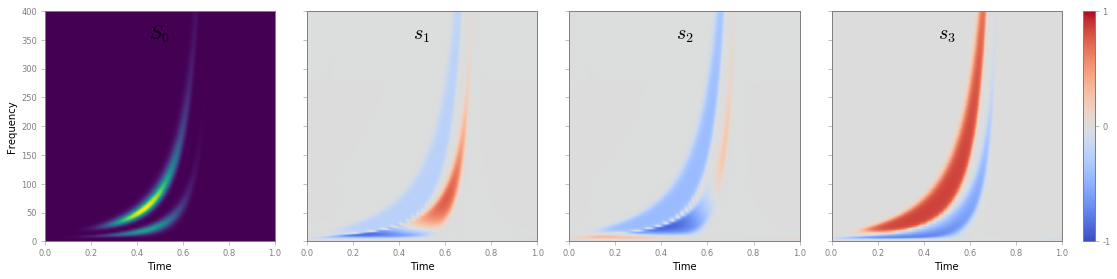
The two representations are equivalent and provide the same information: time, frequency and polarization properties of the bivariate signal. A direct inspection shows that instantaneous parameters of each components are recovered by both representations.
Quaternion Continuous Wavelet Transform (Q-CWT) example¶
The Q-STFT method has the same limitations as the usual STFT, that is not the ideal tool to analyze signals spanning a wide range of frequencies over short time scales. We revisit here the classic two chirps example in its bivariate (polarized) version.
As before, let us first define some constants:
N = 1024 # length of the signal
# hyperbolic chirps parameters
alpha = 15*np.pi
beta = 5*np.pi
tup = 0.8 # set blow-up time value
Now, let us define the instantaneous amplitudes, orientation, ellipticity and phase of each linear chirp. The chirps are also windowed.
t = np.linspace(0, 1, N) # time vector
# chirp 1 parameters
theta1 = -np.pi/3 # constant orientation
chi1 = np.pi/6 # constant ellipticity
phi1 = alpha/(.8-t) # hyperbolic chirp
# chirp 2 parameters
theta2 = 5*t # rotating orientation
chi2 = -np.pi/10 # constant ellipticity
phi2 = beta/(.8-t) # hyperbolic chirp
# envelope
env = np.zeros(N)
Nmin = int(0.1*N) # minimum value of N such that x is nonzero
Nmax = int(0.75*N) # maximum value of N such that x is nonzero
env[Nmin:Nmax] = bsp.utils.windows.hanning(Nmax-Nmin)
Construct the two components and sum it. Again we use the function
utils.bivariateAMFM to compute directly the quaternion embeddings of
each linear chirp.
x1 = bsp.signals.bivariateAMFM(env, theta1, chi1, phi1)
x2 = bsp.signals.bivariateAMFM(env, theta2, chi2, phi2)
x = x1 + x2
Let us visualize the resulting signal, x[t]
fig, ax = bsp.utils.visual.plot2D(t, x)
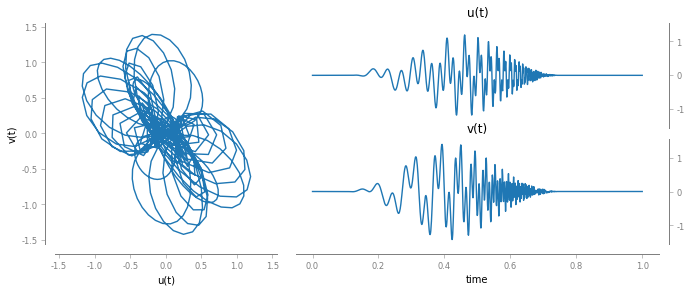
Now, we can compute its Q-CWT. First define the wavelet parameters and initialize the QCWT object:
waveletParams = dict(type='Morse', beta=12, gamma=3)
S = bsp.timefrequency.QCWT(x, t)
And compute:
fmin = 0.01
fmax = 400
S.compute(fmin, fmax, waveletParams, N)
Computing Time-Frequency Stokes parameters
Let us have a look at Time-Scale Stokes parameters S1, S2 and S3
fig, ax = S.plotStokes()
Similarly we can compute the instantaneous polarization attributes from the ridges of the Q-CWT.
S.extractRidges()
Extracting ridges
Ridge added
Ridge added
2 ridges were recovered.
And plot the results
fig, ax = S.plotRidges(quivertdecim=40)
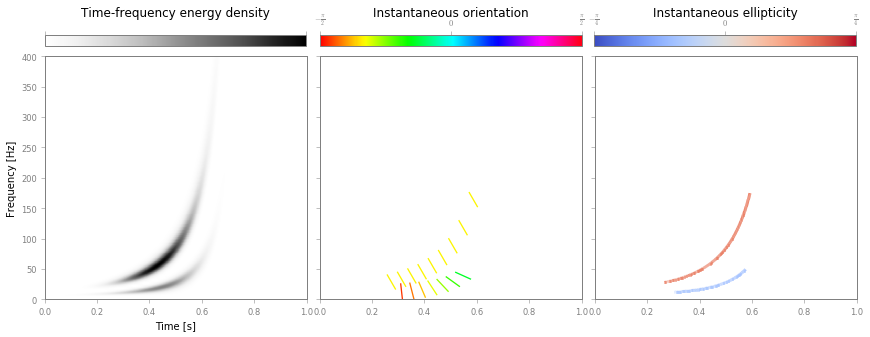
Again, both representations are equivalent and provide the same information: time, scale and polarization properties of the bivariate signal. A direct inspection shows that instantaneous parameters of each components are recovered by both representations.